|
 |
| 1. |
Halle dos números positivos cuya suma sea 20 y cuyo
producto tenga el mayor valor posible. |
|
 |
|
PROCEDIMIENTO PARA RESOLVER EL PROBLEMA: |
|
 |
| |
 |
SOLUCIÓN: |
|
 |
| |
|
PASO 1:
Leer y Analizar detenidamente el Problema
Planteado: |
|
 |
| |
|
Se busca optimizar a
P, el cual es el producto de dos variables.
También, se desea que el producto de estas dos cantidades sea maximizado.
Más aún, la suma de tales variables debe ser
20.
|
|
 |
| |
|
PASO 2:
Trazar un Gráfico, Dibujo, o
Diagrama, con sus respectivos Rótulos: |
|
 |
| |
|
No aplica. |
|
 |
| |
|
PASO 3:
Identificar las Variables que
se habrán de Optimizar, Asignando Símbolos, o Letras, (Notación) a Éstas: |
|
 |
| |
|
 |
NOTACIÓN - Símbolos y su Significado: |
|
 |
| |
|
|
Sea x
y y
aquellas cantidades (variables, o mediciones) que sumadas entre sí
resultan en P, o el producto,
el cual es
20. Nótese, que se desea
maximizar P, o el producto.
Entonces, |
|
 |
| |
|
|
x = Primera variable
identificada |
P
= Producto =
20
(Variable para Maximizar) |
| |
|
|
y = Segunda variable
identificada |
|
|
 |
| |
|
PASO 4:
Determinar la Ecuación Primaria,
la cualue posea la Variable que se habrá Optimizar: |
|
 |
| |
|
 |
La Suma del Primero más el Segundo será 20,
donde el PRODUCTO es un Máximo: |
|
 |
| |
|
|
P
= xy :ECUACIÓN:
Principal :ECUACIÓN:
Principal
 El Producto, P
, es un Máximo
El Producto, P
, es un Máximo |
|
 |
| |
|
|
Se dice que ésta expresión algebraica representa la
ecuación principal por la
razón de que provee el algoritmo requerido para optimizar la cantidad, o
variable, deseada. En otras palabras, esta expresión provee la
ecuación para la cantidad, o variable, que se habrá de optimizar, la
cual es P.
En este caso, el producto será un máximo.
Nótese, que la cantidad, o variable, que se desea optimizar se encuentra
a la izquierda de la ecuación
primaria. Entonces, según fue mencionado arriba, la variable que
se necesita optimizar es
P. |
|
 |
| |
|
PASO 5:
Determinar la Ecuación
Secundaria: |
|
 |
| |
|
 |
La Suma de la Primera Variable más la Segunda,
será 20: |
|
 |
| |
|
|
x +
y =
20 :ECUACIÓN:
Secundaria :ECUACIÓN:
Secundaria
 La Suma de las dos Variables es 20
La Suma de las dos Variables es 20 |
|
 |
| |
|
|
Observe que se requieren las ecuaciones auxiliares
para poder dejar una sola variable en el lado derecho de la ecuación
principal. En otras palabras, tales ecuaciones de apoyo nos
permiten ¨agarrar¨ una de las variables, de manera que sea posible
traducir la ecuación primaria.
Entonces, analizando el problema planteado, como la suma de dos
cantidades, o variables, equivale a
20,
tenemos, pues, que la ecuación auxiliar puede ser
x +
y =
20. |
|
 |
| |
|
PASO 6:
Expresar la Ecuación Primaria
como una Función de la Variable que se habrá de Optimizar: |
|
 |
| |
|
 |
Escribir la Función en Términos de una
Variable: Despejar por y: |
|
 |
| |
|
|
Para aislar una variable, se despeja la ecuación de
apoyo: |
|
 |
| |
|
|
x +
y =
20 :ECUACIÓN:
Secundaria :ECUACIÓN:
Secundaria |
| |
|
|
y =
20 -
x
 :PROPIEDAD:
Aditiva:
de las
Ecuaciones :PROPIEDAD:
Aditiva:
de las
Ecuaciones |
|
 |
| |
|
|
Nótese, pues, que, en la ecuación principal, si una
cantidad, o variable, es x,
entonces, la otra cantidad, o la variable y,
debe ser: (20 -
x).
Su producto, P,
es: P
= x(20
- x) =
20x
- x2.
Entonces, para llegar a este resultado, tenemos que realizar las
siguientes operaciones: |
|
 |
| |
|
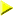 |
Evaluar la Ecuación Primaria en
y:
y
= 20
- x |
|
 |
| |
|
|
P
= xy :ECUACIÓN:
Principal :ECUACIÓN:
Principal |
| |
|
|
P
= x(20
- x) :EVALUACIÓN:
Ecuación:
Principal: P
(x)
= x(20
- x) :EVALUACIÓN:
Ecuación:
Principal: P
(x)
= x(20
- x)
 Función de las Variables que se desea Optimizar
Función de las Variables que se desea Optimizar |
| |
|
|
P
= 20x
- x1+1 :PROPIEDAD:
Distributiva
de la Multiplicación
sobre la Resta :PROPIEDAD:
Distributiva
de la Multiplicación
sobre la Resta |
| |
|
|
 :SIMPLIFICAR:
Multiplicación:
Exponentes: Bases
Iguales: Suman
Exponentes: Pasa la Base:
a1(a1)
= a1+1 = a2 :SIMPLIFICAR:
Multiplicación:
Exponentes: Bases
Iguales: Suman
Exponentes: Pasa la Base:
a1(a1)
= a1+1 = a2 |
| |
|
|
P
= 20x
- x2 :SIMPLIFICAR:
Suma: de:
Exponentes :SIMPLIFICAR:
Suma: de:
Exponentes |
|
 |
| |
|
|
Ahora, tal expresión algebraica se puede describir
como una función de la variable que se desea optimizar: |
|
 |
| |
|
|
P
(x) =
20x
- x2 :ECUACIÓN:
Resultante:
como Función
de la Variable
que se desea
Optimizar :ECUACIÓN:
Resultante:
como Función
de la Variable
que se desea
Optimizar |
|
 |
| |
|
|
Lo que se busca es que el valor, o valores, de
x, como parte de
P
(x) =
20x
- x2,
sean lo más grande posibles. Expresado de otra manera, según el
problema de optimización, el objetivo es Maximizar el producto. |
|
 |
| |
|
PASO 7:
Halle el Dominio para la
Función: P
(x) =
x(20
- x) |
|
 |
| |
|
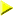 |
Dominio de
P
(x): |
|
 |
| |
|
|
 |
Intervalo Cerrado:
[0,20] |
|
 |
| |
|
|
|
El dominio de
P
(x) es un
intervalo cerrado: 0
≤ x
≤ 20. |
|
 |
| |
|
PASO 8:
Determinar los Valores Óptimos
(Máximos o Mínimos) de la Función que se Habrá de Optimizar: |
|
 |
| |
|
Debido a que el dominio es un intervalo cerrado:
[0,10], el procedimiento se describe a continuación: |
|
 |
| |
|
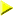 |
Hallar la Primera Derivada: de la Función
P
(x) =
20x
- x2:
P
'
(x) |
|
 |
| |
|
|
P
(x) =
20x
- x2 :ECUACIÓN:
Resultante:
como Función
de la Variable
que se desea
Optimizar :ECUACIÓN:
Resultante:
como Función
de la Variable
que se desea
Optimizar |
| |
|
|
P
'
(x) =
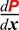 [20x
- x2]
[20x
- x2] :ECUACIÓN:
Resultante:
como Función
de la Variable
que se desea
Optimizar:
Utilizando la:
Notación de Leibniz :ECUACIÓN:
Resultante:
como Función
de la Variable
que se desea
Optimizar:
Utilizando la:
Notación de Leibniz |
| |
|
|
P
'
(x) =
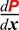 [20x
- 1x2]
[20x
- 1x2] :DEFINICIÓN:
Uno:
como Coeficiente
de una Variable:
a
=
1a :DEFINICIÓN:
Uno:
como Coeficiente
de una Variable:
a
=
1a |
| |
|
|
P
'
(x) =
(1)20x1-1
-(2)1 x2-1 :REGLA:
de la:
Potencia :REGLA:
de la:
Potencia |
| |
|
|
P
'
(x) =
20x1-1
- 2 x2-1 :SIMPLIFICAR:
Multiplicación :SIMPLIFICAR:
Multiplicación |
| |
|
|
P
'
(x) =
20x0
- 2 x1 :SIMPLIFICAR:
Resta:
de Exponentes :SIMPLIFICAR:
Resta:
de Exponentes |
| |
|
|
P
'
(x) =
20(1)
- 2x1 :DEFINICIÓN:
Cero:
como Exponente:
a0
= 1 :DEFINICIÓN:
Cero:
como Exponente:
a0
= 1 |
| |
|
|
P
'
(x) =
20 -
2x :PROPIEDAD:
Elemento Identidad:
en la Multiplicación:
a(1)
= a :PROPIEDAD:
Elemento Identidad:
en la Multiplicación:
a(1)
= a |
| |
|
|

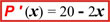  :SOLUCIÓN:
Derivada:
de:
P
(x) =
20x
- x2 :SOLUCIÓN:
Derivada:
de:
P
(x) =
20x
- x2 |
|
 |
| |
|
 |
Determinar los
Números Críticos (Números de Partición) - Integrantes,
o Valores, de la Coordenada-de-x
(Dominio): |
|
 |
| |
|
|
 |
Establecer cuando la primera derivada no está
definida:
P
'
(x) No
Existe: |
|
 |
| |
|
|
|
 |
Debido a que esta es una función polinómica, donde
siempre existe el límite (y es continua), podemos reeplazar a x
en
P
'
(x) =
20 -
2 x
por cualquier número real. |
| |
|
|
|
 |
Por lo tanto,
P
'
(x) existe
para todos los números reales. |
|
 |
| |
|
|
 |
Identificar los valores donde la primera derivada, de
la función
P,
es cero (ceros de la función derivada):
P
'
(x) =
0: |
|
 |
| |
|
|
|
P
'
(x) =
20 -
2x :FUNCIÓN:
Primera
Derivada :FUNCIÓN:
Primera
Derivada |
| |
|
|
|
0
=
20 -
2x :IGUALAR
A CERO:
la
Función Derivada:
Factor
del Numerador :IGUALAR
A CERO:
la
Función Derivada:
Factor
del Numerador |
| |
|
|
|
2x
=
20
 :PROPIEDAD:
Aditiva:
de las: Ecuaciones :PROPIEDAD:
Aditiva:
de las: Ecuaciones |
| |
|
|
|
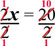  :PROPIEDAD:
Multiplicativa:
de las: Ecuaciones :PROPIEDAD:
Multiplicativa:
de las: Ecuaciones |
| |
|
|
|
x
=
10 :SIMPLIFICAR:
Cancelación:
División Simultanea
entre
Factores Comunes :SIMPLIFICAR:
Cancelación:
División Simultanea
entre
Factores Comunes |
| |
|
|
|

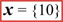
 :CONJUNTO
SOLUCIÓN:
Número
Crítico:
x
=
10 :CONJUNTO
SOLUCIÓN:
Número
Crítico:
x
=
10 |
|
 |
| |
|
|
|
Como se puede observar, la primera derivada se
encuentra en cada punto del intervalo 0
≤ x
≤ 20
y es igual a cero cuando x
=
10.
|
|
 |
| |
|
 |
Determinar los
Valores Críticos (Coordenada en el eje-de-y,
o Rango) de la Función, Correspondientes a sus Números Críticos -
Establecer los Valores Extremos Relativos: |
|
 |
| |
|
|
 |
Determinar el Valor Extremo Relativo/local, máximo
o mínimo, que Asume la Función en su Número Crítico:
Valor, o Coordenada, Localizado en el eje-de-y: |
|
 |
| |
|
|
|
 |
Evaluar los Posibles Números Críticos en la Función
Original: Sustituir los Números Críticos Dentro de la Función
Original: |
|
 |
| |
|
|
|
|
P
(x) =
20x
- x2 :ECUACIÓN:
Resultante:
como Función
de la Variable
que se desea
Optimizar :ECUACIÓN:
Resultante:
como Función
de la Variable
que se desea
Optimizar |
| |
|
|
|
|
P
(10) =
20(10)
- (10)2 :EVALUACIÓN:
en:
Función Original:
Número Crítico:
x
=
10 :EVALUACIÓN:
en:
Función Original:
Número Crítico:
x
=
10 |
| |
|
|
|
|
P =
200 -
100 :SIMPLIFICAR:
Multiplicación :SIMPLIFICAR:
Multiplicación |
| |
|
|
|
|
P =
100 :SIMPLIFICAR:
Resta :SIMPLIFICAR:
Resta |
| |
|
|
|
|
 P =
100
P =
100 :SOLUCIÓN:
Punto
para el: Valor
Crítico:
y
=
100 :SOLUCIÓN:
Punto
para el: Valor
Crítico:
y
=
100
 P =
100
P =
100 |
| |
|
 |
Evaluar a
P
en Todos los Extremos - Determinar los
Valores Extremos: |
|
 |
| |
|
|
P
(0) =
0 |
| |
|
|
P
(20) =
0 |
|
 |
| |
|
PASO 9:
Plantear el Resultado en el
Contexto del Problema Original: |
|
 |
| |
|
El valor máximo del producto,
P,
es 100:
P =
100.
Lo dos números positivos, donde sus sumo equivale a 20, son, a saber:
x
=
10
y
20 - 10 = 10. |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|