La cinética es aquella parte de la mecánica que describe las fuerzas que causan los movimientos, tales como las fuerzas de gravedad, muscular, fricción y resistencia externa. El estudio de las fuerzas que causan el movimiento lineal representa la cinética lineal.

Concepto

        La fuerza es todo aquello que empuja o hala a través del contacto mecánico directo o por medio de la fuerza de gravedad, lo cual puede alterar el estado de reposo de un objeto u cuerpo y su movimiento uniforme en línea récta. Representa una cantidad física que puede acelerar y/o deformar un cuerpo, un segmento de éste o un objeto.
        La tensión es un sistema de fuerzas que tienden a separar las partes de un cuerpo, combinadas con fuerzas iguales y opuestas que contribuyen a mantener la unión de las partes. Sus unidades de medición son los kilogramos (kg) o las dinas. En fisiologia, los términos tensión y fuerza se usan intercambiablemente, i.e., son sinónimos. Por ejemplo, la tensión intramuscular es la fuerza de contracción muscular. La Fuerza de un músculo es su capacidad para generar tensión.

Unidades de Medida para Fuerza y Masa (Peso)

Sistema Métrico

        Como unidades de fuerza tenemos:

        Newton (N). Esta unidad representa aquella fuerza que le imparte una aceleración de un (1) metro (m) por segundo por segundo (1 m/seg²) al cuerpo u objeto de una masa de un (1) kilogramo (kg), en dirección a la acción de la fuerza. Es la fuerza requerida para levantar una masa de 0.102 kilogramos (kg) a nivel del mar y a 45 grados de latitud.

        Kilopondio (kp). El kilopondio es aquella fuerza que le imparte una aceleración gravitatoria normal/estándar (9.807 m/seg² ó 32 pies/seg²) a la masa de un (1) kilogramo (kg). Representa la fuerza que ejerce la gravedad sobre la masa de un (1) kilogramo (kg) a una aceleración normal de gravedad (9.807 m/seg² ó 32 pies/seg²).

        Pondio (p). La unidad de pondio representa aquella fuerza que le imparte una aceleración gravitatoria estándar/normal (9.807 m/seg2 ó 32 pies/seg2) a la masa de un (1) gramo (g).

        Como unidad de masa/peso, tenemos las siguientes

        Kilogramo (kg). Es aquella unidad del sistema métrico que determina la cantidad de masa en un cuerpo u objeto.

Sistema Inglés

        Bajo las unidades del sistema anglosajón, se emplea la libra (lb) como una medida para determinar la cantidad de masa en un cuerpo u objeto. El peso de una libra estándar a nivel del mar y a 45 grados de latitud.

Equivalencias/Factores de Conversión

        La fuerza se puede categorizar como aquellas internas y las externas. Las fuerzas internas son las que actúan sobre estructuras del cuerpo. Por ejemplo, la tracción del músculo sobre el hueso. Este tipo de fuerza produce diferencias en el aspecto del cuerpo. Por otro lado, las fuerzas externas son aquellas que se imparten fuera del organismo humano. La fuerza de gravedad representa un ejemplo clásico de una fuerza externa. Esta fuerza induce el desplazamiento del cuerpo.

Componentes de la Fuerza

        La fuerza es un vector. Esto implica que posee magnitud, dirección y un punto de aplicación, donde se imparte la fuerza.

Magnitud/Intensidad

        Concepto. Seleccionemos a la fuerza de gravedad. Ésta es un tipo de fuerza externa que el cuerpo humano debe sostener y contrarrestar en todas las experiencias de movimiento. La masa corporal (peso del cuerpo) es un ejemplo donde actúa este tipo de fuerza. Su ecuación es la siguiente:

STF	=	Grosor del Músculo X
		Longitud # Líneas Cortan  cada Fibra

Problema (Busque):

Dado:

Grosor del Músculo  =  Longitud de las líneas que cortan perpendicularmente cada fibra:   1er   =   4 pulg. 2da  =  5 pulg. 3ra  =  3 pulg.

Conocido:

        Sección Trasnsversal Fisiológica (STF):

STF	=	Grosor del Músculo X
		Longitud # Líneas Cortan  cada Fibra

STF   =   (4  +  5  +  3)           =  (12)           =  9 STF  =  9 pulgadas cuadradas

        Se refiere al punto en el cual se aplica la fuerza al objeto. Cuando la fuerza de gravedad esta involucrada, este punto se aplica siempre a través del centro de gravedad de un objeto. En los músculos esqueléticos del cuerpo humano, el punto de aplicación de la fuerza muscular representa aquel punto de insersión muscular entre la línea de fuerza (o tracción) y el eje mecánico de un hueso o segmento que sirve como palanca anatómica.

Dirección

        Concepto. La dirección representa la fuerza transmitida a lo largo de su línea de acción (representada por un vector), la cual se dirige hacia abajo (debido a la fuerza de gravedad) y que comienza desde el centro degravedad del objeto.

        Componentes. La dirección de la fuerza se encuentra constituída por la línea de aplicación de la fuerza y el sentido de la fuerza.

        Dirección de la fuerza muscular. Representa la dirección de la línea de tracción (o acción) del músculo. Se identifica mediante el ángulo que se forma durante la tracción del músculo. El ángulo de tracción de un músculo se compone de la línea de tracción del músculo y la porción del eje mecánico ubicado entre el punto de aplicación y el fulcro (eje o punto de pivote). En el cuerpo humano la fuerza producida por un músculo actúa en la dirección longitudinal del tendón de ese músculo.

Descripción Gráfica de la Fuerza

        Como fue previamente mencionado, la fuerza es una cantidad vectorial, de manera que, posee las cualidades de magnitud y dirección. Por lo tanto, la fuerza se representa por una flecha dibujada a escala. Tenemos, entonces, que:

• La base (cola) de la flecha: Indica el punto de aplicación de la fuerza.
• Orientación/dirección de la flecha: Representa la línea de aplicación de la fuerza (la dirección de la flecha).
• La punta de la flecha: Muestra el sentido de la fuerza.
• El largo/longitud de la flecha: Representa la magnitud/intensidad de la fuerza.
• Extensión de la flecha en cualquier dirección: Representa una extensión de la línea de aplicación.

        Los objetivos para la resolución de fuerzas es: (1) visualizar el efecto que tienen esas fuerzas en el cuerpo y (2) calcular la magnitud de las fuerzas que producen los músculos y las fuerzas de compresión de la articulación.
        Para determnar la cantidad vectorial que representa la fuerza, sabemos que gráficamente:
(1) la magnitud de la fuerza representa el largo de la línea vectorial, (2) el punto de aplicación de la fuerza es el punto donde la fuerza vectorial comienza y (3) la dirección de la fuerza aplicada respresenta la tracción hacia afuera desde el punto de aplicación (la flecha del vector).

Ángulo de Tracción

        Se ha establecido como un principio que cuando una fuerza actúa en ángulo en un segmento, esa fuerza puede resolverse en dos fuerzas componentes, una vertical y otra horizontal. Esto implica que una fuerza se resuelve en los siguientes componentes:

• Componente vertical (eje o coordenada-y) (Fy): Es perpendicular () al eje de x.
• Componente horizontal (eje o coordenada-x) (Fx): Es paralelo al eje de x.
• Fuerza original (resultante) (R ó Fx): Se deriva de la combinación de las fuerzas vertical y horizontal.

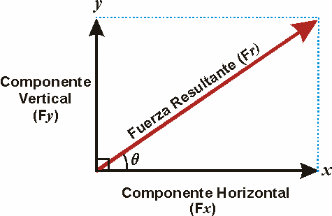
La magnitud y la direccion de estos componentes tienen el mismo efecto que la fuerza original. Otros componentes del ángulo de tracción incluyen los siguientes:

• Componente rotatorio, vertical (Fy) u opuesto (O): Componente  al segmento o palanca (eje x) que es la fuerza efectiva en causar el movimiento rotatorio del segmento alrededor de un eje.
• Componente paralelo, horizontal (Fx) o adyacente (A): Componente paralelo al segmento o palánca ósea (o el eje de-x) que causa compresión o distracción entre las superficies articulares.

• Lado opuesto (O) al ángulo () agudo considerado (i.e. el ángulo de tracción en el caso de las fuerzas vectoriales del músculo).
• Lado adyacente (A) al ángulo () agudo considerado (i.e. el ángulo de tracción en el caso de las fuerzas vectoriales del músculo).
• La hipotenusa (H), la cual representan el lado opuesto al ángulo rectángulo (90°) y siempre es el lado más largo en un triángulo rectángulo.

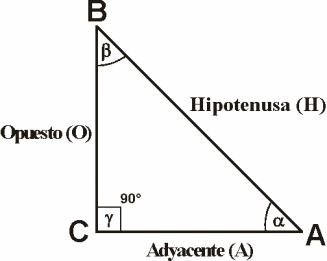
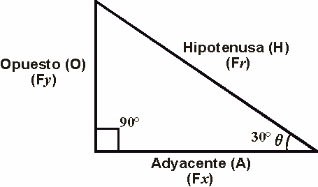
        AB y C son los vértices de de este triángulo. Si el ángulo  (vértice A) es el que será considerado, entonces, el lado AC es el adyacente (A) y el lado BC el opuesto (O). La hipotenusa (H) sería el lado AB. La suma de los tres ángulos de un triángulo es igual a 180 ° (  +   +   = 180°). Dos ángulos se dedominan complementarios cuando su suma es igual a 90°. En un triángulo rectángulo, los dos ángulos entre lla hipotenusa y los lados adyacentes son complementarios (  +    = 90°). La suma de los cuadrados de los lados de un triaángulo rectángulo es igual al cuadrado de la hipotenusa (teorema de Pitágoras):

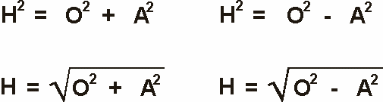
        Las funciones trigonométricas se definen como sigue:

• El seno de un ángulo en un triángulo rectángulo es igual al opuesto dividido por la hipotenusa y es igual al coseno del ángulo complementario:

Opuesto           BC sen   =   -------------  =  -------  =  cos  =  (90°  - )                    Hipotenusa         AB

• El coseno de un ángulo en un triángulo rectángulo es igual al adyacente dividido por la hipotenusa y es igual al seno del ángulo complementario:

Adyacente           AC cos   =   -------------  =  -------  =  sen  =  (90°  - )                    Hipotenusa         AB

• La tangente de un ángulo en un triángulo rectángulo es igual al opuesto dividido por la adyacente:

Opuesto           AC tan   =   -------------  =  -------  =  sen =  (90°  - )                   Adyacente        AB

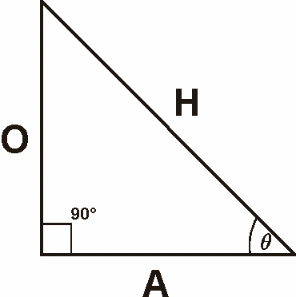
LADO OPUESTO:	LADO ADYACENTE
O sen   =   ------               H O  =  (sen ) H	A cos   =   ------               H A  =  (cos ) H

O tan   =   ------               A                  A cotan   =   ------                  O

sen  =  (90  -  0)                  sen  tan   =   -------                   cos

        Para calcular la magnitud de cada uno de los componentes de las fuerzas previamente descritos, se utilizan las funciones en un ángulo (trigonométricas), tal como el teorema de pitágoras (o ley de los cosenos), donde la hipotenusa es la fuerza original. El tamaño relativo de los componentes vertical y horizontal se encuentra determinadio por el ángulo en el cual la fuerza es aplicada.

        Analizando la acción musculo-esquelética. El tamaño del ángulo de tracción del músculo cambia con cada grado del movimiento articular. Esto implica que también cambian los tamaños de los componentes horizontal y vertical. Entre mayor sea el ángulo entre 0 y 90 grados, mayor será el componente vertical y menor el componente horizontal.
        El componente rotatorio representa el componente vertical de la tracción del músculo. Es siempre perpendicular a la palanca. Es aquella parte de la fuerza que mueve la palanca. El componente no rotatorio representa el componente horizontal. Es paralelo a la palanca. Cuando la línea de tracción es de 90 grados, la fuerza es completamente rotatoria. Cuando la línea de tracción es 45 grados, los componentes rotatorios y estabilizadores son iguales.
        A continuación un problema/ejercicio que demuestra el efecto del ángulo de tracción sobre una fuerza rotatoria de un músculo para un ángulo dado:

Problema  - Busque:

Dado:

Conocido:

        Seno del ángulo () agudo en consideración:

Opuesto           O sen   =   -------------  =  -------                    Hipotenusa          H

        Coseno del ángulo () agudo en consideración:

Adyacente           A cos   =   -------------  =  -------                    Hipotenusa          H

• A un ángulo de tracción de 10°:

• Componente Rotatorio o Fy (Opuesto):

Opuesto           O                          Opuesto sen   =   -------------  =  -------   =  seno 10°   ------------                   Hipotenusa          H                         100 lb Componente Rotatorio  =  (100)  (seno 10°)                               =  (100)  (0.1736)                               =  17.36 lb

• Componente Estabilizador o Fx (Adyacente):

Adyacente           A                        Adyacente cos  =   -------------  =  -------   =  cos 10°   ------------                   Hipotenusa          H                          100 lb Componente Estabilizador  =  (100)  (cos 10°)                                    =  (100)  (0.9848)                                    =  98.48 lb

• A un ángulo de tracción de 30°:

• Componente Rotatorio o Fy (Opuesto):

Opuesto           O                         Opuesto sen  =   -------------  =  -------   =  seno 30°   ------------                   Hipotenusa          H                          100 lb Componente Rotatorio  =  (100)  (seno 30°)                               =  (100)  (0.5000)                               =  50.0 lb

• Componente Estabilizador o Fx (Adyacente):

Adyacente           A                       Adyacente cos   =   -------------  =  -------   =  cos 30°   ------------                   Hipotenusa          H                         100 lb Componente Estabilizador  =  (100)  (cos 30°)                                    =  (100)  (0.8660)                                    =  86.6 lb

• A un ángulo de tracción de 75°:

• Componente Rotatorio o Fy (Opuesto):

Opuesto           O                         Opuesto sen   =   -------------  =  -------   =  seno 75°   ------------                   Hipotenusa          H                           100 lb Componente Rotatorio  =  (100)  (seno 75°)                               =  (100)  (0.9659)                               =  96.59 lb

• Componente Estabilizador o Fx (Adyacente):

Adyacente           A                     Adyacente cos   =   -------------  =  -------   =  cos 75°   ------------                   Hipotenusa          H                         100 lb Componente Estabilizador  =  (100)  (cos 75°)                                    =  (100)  (0.2588)                                    =  25.88 lb

        Concepto. Es generalmente un carrete con una cuerda corriendo sobre éste. La polea es una rueda acanalada en su circumferencia, que gira alrededor de un eje fíjo por la acción de una cuerda que pasa alrededor de ella. El eje es sostenido por un armazón. Todo el conjunto puede usarse en forma de polea fija, o polea móvil.

        Función. Se utilizan para cambiar la dirección de una fuerza ó para aumentar ó disminuir la magnitud de la fuerza.

        Poleas anatómicas. En el cuerpo no tenemos poleas como tal pero tenemos unas prominencias oseas y otros medios. Los objetivos/propósitos (funciones) de las poleas son cambio de dirección y mejorar la ventaja mecánica. La poleas trabaja para desviar/cambiar la dirección de la fuerza de un músculo. Esto ocurre al cambiar el ángulo de tracción de un músculo, el cual ejerce su fuerza durante la contracción. La ventaja mecánica del músculo puede aumentar mediante el empleo de poleas. Básicamente, esto es posible al aumentar su brazo de esfuerzo (distancia perpendicular desde la línea de acción del músculo y el eje de movimiento de la articulación). Por ejemplo, la rótula (o patela) aumenta el ángulo de tracción de los músculos cuadriceps según cruza por el frente de la rodilla (en otras palabras, cambia la dirección de la línea de acción del cuadriceps y aumenta el largo del brazo del esfuerzo del cuadriceps (palancaje). Esto incrementa el componente de la fuerza rotatoria por parte de los cuadriceps.
        En el organismo humano existen diversos tipos de poleas en el cuerpo humano. Por ejemplo, el sistema musculoesqueletal cuenta con poleas anatómicas fijas y sencillas. Las poleas sencillas tienen la tarea de cambiar la línea de una fuerza. Existen también poleas movibles, las cuales se encargan de distribuir el peso que se está levantando a través de un número de cuerdas. Por lo tanto, estos tipos de poleas proveen un aumento en la ventaja mecánica.

Resolución de Fuerzas Externas

        La resolución de fuerzas externas se lleva a cabo en la misma manera que fue explicado con las fuerzas musculares. Podría ser utilizada cuando la fuerza se aplica a un ángulo oblicuo. Este es el caso cuando se empuja una mesa diagonalmente. La fuerza se aplica en un águlo ablicuo, por lo que posee ambos componentes de fuerza (vertical y horizontal), donde:

El determinate para que se pueda mover la mesa es el componente horzontal, i.e., la cantidad total de fuerza aplicada en la dirección horizontal.

Efectos Compuestos de Dos o más Fuerzas

         Comunmente, las fuerzas trabajan en conjunto con otras, particularmente en pares. Dado esto, existen varias formas en las actúan las fuerzas. Éstas pueden ser lineales, concurrentes o paralelas.

Fuerzas Lineales

        Concepto. Son aquellas fuerzas aplicadas en la misma dirección a lo largo de la misma línea de acción. Representan dos fuerzas que actúan en la misma dirección, y se aplican en el mismo punto. Son equivalentes a una fuerza simple actuando en aquella dirección, y cuya magnitud/intensidad es igual a la suma de las magnitudes/intensidades de cada una de las fuerzas.

        Ejemplos. Un par fuerzas lineales pueden ser impartidas hacia un a misma dirección o en sentidos opuestos, una de la otra.:

• Dos fuerzas aplicadas a un mismo cuerpo/objeto: La resultante (c) de las dos fuerzas es igual a la suma de las dos fuerzas (a  +  b  =  c).

• Dos fuerzas que actúan en direcciones opuestas a un mismo cuerpo u objeto:  La resultante (c) de las dos fuerzas es igual a la resta de las dos fuerzas (a  -  b  =  c).

Fuerzas Concurrentes

        Concepto. Puede ser descritas como aquellas fuerzas actuando en el mismo punto pero a diferentes ángulos.

        Principios. De las fuerzas concurrentes se pueden se pueden desprender los siguientes principios:

• Dos fuerzas iguales actuando sobre un punto común, y en direcciones opuestas producirán un estado de equilibrio.
• Dos fuerzas desiguales actuando sobre un punto común, y en direcciones opuestas producirán un movimiento en la dirección de la fuerza mayor. La intensidad de la fuerza que producirá este movimiento será igual a la diferencia entre las intensidades de las dos fuerzas desiguales que se oponen entre si.
• La resultante de dos o más fuerzas concurrentes dependerá de la magnitud de cada fuerza y el ángulo de aplicación (la dirección de cada fuerza).

        Concepto. Son aquellas fuerzas paralelas a la línea de acción que actúan en diferentes puntos sobre el cuerpo. El efecto de las fuerzas paralelas sobre un objeto dependerá de la magnitud, dirección y el punto de aplicación de la fuerza.

        En esta sección estaremos discutiendo las tres leyes postuladas por Newton. Estas leyes son, a saber: (1) la ley de inercia (primera ley de Newton), (2) ley de aceleración (segunda ley de Newton) y (3) ley de acción-reacción (tercera ley de Newton).

Ley de Inercia

Concepto

        La ley de inercia postula que un cuerpo en reposo permanecerá en reposo y un cuerpo en movimiento continuará moviendose en línea recta y a una velocidad constante a menos que fuerzas externas modifiquen su estado. Podemos describir el concepto de inercia como:

• La propiedad de un objeto que causa que se mantenga en su estado de reposo o movimiento.
• La resistencia de un cuerpo a toda variación en su estado de movimiento o de reposo.
• La fuerza efectiva inversa de un cuerpo.

Ejemplo

        Una vagoneta colocada en un suelo o carril horizontal requerirá la aplicación de una fuerza considerable para ponerla en movimiento, pero una vez conseguido este objetivo continuará moviéndose hasta que otra fuerza, como por ejemplo la colisión con los parachoques de otra vagoneta, detenga su progresión. Si en la primera vagoneta iba un hombre de pie, éste será proyectado hacia delante en el momento de la colisión ya que su cuerpo continuará moviéndose a causa de la inercia.

Ley de Aceleración

Concepto

        Esta segunda ley de Newton postula que la aceleracion de un cuerpo/objeto es directamente proporcional a la fuerza que causa la aceleración y es inversamente proporcional a la masa de ese cuerpo/objeto. De esta ley se pueden derivar las siguientes implicaciones:

• Si la aceleración de un cuerpo es directamente proporcional a la fuerza, entonces, entre mayor sea la fuerza aplicada al cuerpo, mayor será la aceleración.
• Si la aceleración de un cuerpo es inversamente proporcional a la masa de un cuerpo, entonces, entre mayor sea la masa (o inercia) de un cuerpo, menor será la aceleración en respuesta a una fuerza aplicada dada.

P = m  x  g ;    m  =

P -----   g

Ecuación

        Matemáticamente, la ley de aceleración se puede describir en términos de la relación entre la fuerza, aceleración y masa:

F a   -------        ó             m

F  m  x  a

        Cuando se le asignan unidades de fuerza, masa y aceleración, la relación de estos factores significa que puede expresar como sigue:

        A continuación de describe un ejemplo para determinar la fuerza neta externa:

Problema (Busque):

Dado:

Conocido:

        Concepto. El impulso de un cuerpo es la cantidad de movimiento que posee. Está representado por el producto de la masa y la velocidad, i.e, el producto de la fuerza y el tiempo sobre la cual actúa (Ft).

        Principios/implicaciones. A raíz de lo que postula el concepto de impulso, podemos derivar los siguinetes principios:

• La fuerza responsable de este impulso producirá un movimiento lento en un cuerpo relativamente pesado.
• El movimiento será más rápido en un cuerpo más ligero.

Momentum

        Concepto. El producto de la masa y velocidad (mv). Es una cantidad de movimiento que puede aumentar o reducirse al aumentar o reducir la masa o la velocidad. Entre mayor sea la masa o peso (fuerza) de un cuerpo en movimiento y/o mayor sea el tiempo  en que se aplica la fuerza, mayor será su cambio en momentum.

        Ecuación. Matemáticamente, momentum se puede describir como sigue:

        Representación vectorial. Momentum es una cantidad vectorial, i. e., posee dirección, magnitud y un punto de aplicación. Los vectores se visualizan gráficamente por medio de:

• Una línea de acción. La línea de acción se dibuja en una escala arbitraria para representar la magnitud de la fuerza.
• Con una flecha que nos indica la direccion de esa fuerza.
• Con un punto de aplicación que representa la aplicación de una fuerza en un cuerpo.

Concepto

        La tercera ley de Newton postula que para cada acción siempre hay una reacción igual y opuesta. Esto quiere decir que, por ejemplo, un velocista puede aumentar su velocidad de los bloques de salida si aumenta su fuerza contra éstos.

Conservación del Momentum

        Conocida también como la ley de la conservación del momentum, postula que un sistema en movimiento continuará moviendose a un momentum constante a menos que una fuerza externa actúe sobre él. En cualquier sistema donde fuerzas actúan una sobre la otra, el momentum se mantiene constante.

Implicaciones Teóricas

• Este principio representa el cambio en momentun cuando el objeto o cuerpo es puesto en movimiento por una fuerza.
• Puesto que la fuerza que causa este cambio en el momentum debe poseer un fuerza igual y opuesta, debe tomar lugar otro cambio en momentum igual u opuesto sobre el objeto o cuerpo que produce la fuerza reactiva.

        Aquí en el planeta tierra, el peso representa el factor de mayor importante que altera el movimiento de un objeto o cuerpo. Otras condiciones que afectan el movimiento son las fuerzas de contacto y las de fluído (o líquido).

Peso

       El peso de de un objeto o cuerpo es el resultado directo de la fuerza de atracción ejercida por la tierra, i.e., las fuerzas gravitacionales. La fuerza de gravedad representa el peso del cuerpo aplicado a través del centro de gravedad del cuerpo y dirigido hacia el eje de la tierra. Como fue previamente descrito, su expresión matemática es la siguiente:

P = m  x  g

         Según fue mencionado previamente, las fuerzas siempre existen en parejas. Las fuerzas que actúan entre dos cuerpos son iguales y actúan en direcciones opuestas (según la Tercera Ley de Newton). Cada vez que hay un empujón debe haber otro empujón opuesto. Las fuerzas de contacto pueden ser de dos tipo: (1) fricción y de (2) elasticidad y rebote.

Fricción

        Concepto. La fricción representa aquella fuerza que se opone al movimiento cuando una superficie se desliza sobre otra. Es la fuerza que opone al esfuerzo para que se deslice o ruede un cuerpo sobre el otro.

        Valor/importancia. La fuerza de fricción nos permite caminar, correr y efectuar
cualquier tipo de movimiento.

        Desventaja. El problema de este tipo de fuerza es que aumenta la dificultad de mover objetos. En ocasiones, se intenta reducir la fricción en ciertos deportes. Un ejemplo de esta situación es la suela de los zapatos de los jugadores de boliche. Esta suelas deben de poseer muy poca fricción, de manera que puedan deslizarse con mayor facilidad durante el acercamiento.

        Tipos de fricciones. Existen dos tipos de fricciones, la dinámica y de limitación. La fricción dinámica se genera a raíz de la resistencia de fricción producida durante el movimiento. Este tipo de fricción es ligeramente menor que la fricción de limitación. Además, Puede reducirse posteriormente durante los movimientos de una extremidad, siempre que éste permanezca apoyado en una superficie plana, por el uso de una superficie pulimentada, como una tabla en la que se deslice la extremidad. Por el ortro lado, la fricción de limitación es aquella que se produce en el preciso momento en que empieza el deslizamiento.

        La cantidad de fricción entre una superficie y la otra. Ésta dependerá de la naturaleza de las superficies y de las fuerzas que presionan ambas superficies. Por ejemplo, las superficies lisas poseen menos fricción que las ásperas/rústicas.

        Principios. Dos principios se derivan de las fuerzas de fricción, a saber:

• La fricción es proporcional a la fuerza que presiona ambas superficies.
• La fuerza de la fricción actúa paralela a las superficies que se deslizan una sobre la otra y opuesta a la dirección del movimiento.

• Para poder reducir la fricción, la aplicación de polvo de talco o de aceite en la superficie de apoyo reducirá sucesivamente la fricción y contribuirá a facilitar el movimiento. En adición, la suspensión de la región que deba moverse eliminará virtualmente toda resistencia de fricción.
• La fricción puede ser suficiente para impedir el movimiento, como en el caso de superficies o substancias rugosas, tales como la goma, cuando se hallan en contacto una con otra.

=

F ---  P

Elasticidad y Rebote

        Coeficiente de elasticidad o restitución. Representa estrés dividido entre esfuerzo ("strain"). Son evidentes en aquellos deportes donde ocurre la compresión de bolas.

        Ángulo de rebote. Como principio, el rebote de un objeto perfectamente
elástico es similar a la reflexion de la luz. Esto implica que el ángulo de incidencia es igual al ángulo de reflexión. El giro ("spin") afecta los ángulos de rebote.

Fuerzas de Fluído (Líquido)

        Dos fuerzas hidrodinámicas prevalecen en los líquidos, a saber, la flotabilidad y  las fuerzas de levante y arrastre.

Flotabilidad

        Concepto. La flotabilidad representan aquellas fuerzas dirigidas hacia arriba que contrabalancean el peso (fuerza) que actúa verticalmente a través del centro de gravedad de un objeto en agua. La magnitud de esta fuerza es igual al peso del agua desplazada por el cuerpo flotante.

        Principio de Arquímedes. Cualquier objeto sólido completamente o parcialmente sumergido en un líquido flotará mediante una fuerza igual al peso del líquido desplazado por el objeto. Esto quiere decir que un cuerpo sumergido en agua se hundirá hasta que el peso del agua que desplaza sea igual al peso del cuerpo. Los objetos que se hunden (flotabilidad negativa) no desplazan la cantidad suficiente de agua para que igualen su peso. Fraseado de otra manera, cuando el volumen de agua desplazado por un objeto o cuerpo pesa menos que el peso del
objeto/cuerpo, el objeto/cuerpo se hundirá. La cantidad de agua desplazada por un objeto o
cuerpo (la fuerza boyante positiva actuando sobre el centro de gravedad del objeto/cuerpo sumergido en el agua) equivale a la diferencia en el peso de un objeto cuando se encuenbra sumergido en agua y el peso de ese mismo objeto determinado fuera el agua. Por el otro lado, el peso del agua que desplaza el objeto o cuerpo equivale al peso total del objeto/cuerpo flotante.

        Componentes de la flotabilidad. Los constituyentes de la flotabilidad son la fuerza boyante y el centro de flotabilidad del objeto.

• Fuerza boyante: Este tipo de fuerza representa la presión que ejerce el agua hacia            arriba contra el volumen/objeto sumergido en el agua. Si la fuerza boyante excede la fuerza de gravedad (en otras palabras, si el peso del objeto/cuerpo es menor que la fuerza boyante máxima), el objeto sube (flota). Por el contrario, si la fuerza de gravedad excede la fuerza boyante (en otras palabras, si el peso del objeto/cuerpo es mayor que la fguerza boyante máxima), entonces,  el objeto se hunde. Ahora bien. si la fuerza de boyante y la de gravedad son iguales, el objeto no subirá ni se hundirá. Las fueza botante provienen de las fuerzas de presión. El factor clave que afectan la fuerza boyante (fuerza hacia arriba neta) es la diferencia entre las fuerzas hacia arriba y las de abajo. Esto equivale al peso del líquido desplazado.

• Centro de flotabilidad del volumen/objeto: Representa el punto a través del cual actúa la fuerza boyante. Es el punto de aplicación de la fuerza boyante.

Levantamiento y Arrastre

        Fuerza de levante. Cuando un cuerpo se mueve a través de un fluído, la fuerza de levante representa aquella fuerza del fluído que se opone al movimiento hacia el frente del cuerpo. Se caracteriza por ser perpendicular a la fuerza de arrastre. Además, induce que el cuerpo se levante conforme se mueve hacia el frente.

Patrones en el Aire y Giro ("Spin") de la Bola

       El patrón de aire que rodea a un objeto, puede ser  liso o turbulento. Según el principio de Bernoilli, la presión en un líquido que se mueve disminuye conforme su velocidad aumenta.

Trabajo

Concepto

        Trabajo es el producto de la cantidad de fuerza aplicada y la distancia a través de la cual la fuerza actúa para contrarestar su resistencia.

Ecuación/Fórmula

        Trabajo realizado por un cuerpo desplazandose en un movimiento lineal:

Unidades de Medida/Expresión

        La unidad de medida empleada para expresar cálculos de Trabajo incluyen la combinación de una unidad de fuerza con una unidad de distancia.  En el sistema Inglés se conocen los: Pies-Libras (pies-lbs). Por el otro lado, en el sistema métrico son comunes los Julios (J). 1 julio equivale a 10² x 1 gramo de fuerza ejercido a través de 1 centímetro.

Ejemplos

        A continuación se presentan dos ejemplos que ilustran la estimación de Trabajo mediante la exposición de dos problemas.

PROBLEMA # 1:

Problema:

Dado:

Conocido:

PROBLEMA # 2:

Problema:

Dado:

Conocido:

Tipos de Trabajo

        Dependiendo de la dirección (a favor o en contra de la fuerza de gravedad) en que se lleva a cabo el trabajo, éste puede ser positivo o negativo.

        Trabajo positivo. Es aquel trabajo efectuado en la misma dirección en que el cuerpo se mueve. Por ejemplo, durante la acción muscular concéntrica de los músculos extensores de las piernas para colocarse de pie desde una posición en cuclillas     (rodillas flexionadas). En esta situación, los músculos extensores de la pierna se contraen concéntricamente, a favor de la fuerza de gravedad. El cuerpo se mueve en la misma dirección que los músculos extensores contraiendose concentricamente.

        Trabajo negativo. Representa aquel trabajo realizado en dirección opuesta al movimiento del cuerpo. Esto se puede observar durante la acción muscular eccéntrica involucrada por parte de los extensores de las piernas al flexionar las rodillas (encuclillarse). En este caso, los músculos extensores de la pierna se contraen eccéntricamente para resistir el efecto de la fuerza de gravedad sobre el cuerpo. El cuerpo se mueve en una dirección opuesta a la fuerza de contracción eccéntrica hacia  arriba que ejercen los músculos de las piernas.

Trabajo Mecánico Realizado por un Músculo Individual

        La mejor manera para explicar el trabajo que puede ejecutar un músculo individual del cuerpo humano es a través de varios ejemplos. Primeramente, haremos un problema donde se conoce la fuerza aplicada por el músculo y luego en un caso donde no se conoce la fuerza.

CASO # 1: CUANDO SE CONOCE LA FUERZA EJERCIDA POR UN MÚSCULO

Problema:

Determinar el trabajo (en pies-libras) efectuado por un músculo rectangular, 4 pulgadas de largo y 1 pulgada de ancho ejerciendo una fuerza de 66 libras mientras mueve angularmente una palanca ósea.

Dado:

Conocido:

CASO # 2: CUANDO NO SE CONOCE LA FUERZA EJERCIDA POR UN MÚSCULO

Problema:

Determinar el trabajo (en pies-libras) efectuado por un músculo rectangular, 4 pulgadas de largo y 1 pulgada de ancho ejerciendo una fuerza de 66 libras mientras mueve angularmente una palanca ósea.

Dado:

Conocido:

DADO:  Fuerza (F) Promedio  =  90 lb/pulg2 Sección Transversal (ST)  =  0.75 pulg2 SOLUCIÓN:  F  =  90 lb/pulg2    x  0.75 pulg2     = 67.5 lb

TRABAJO EN: pulg-lb:  T  =  (67.5 lbs) (2 pulg)     = 135 pulg-lbs TRABAJO EN: pies-lb:              135 pulg-lbs                 1 pie T  =   ------------------   x   ------------                       1                         12 pulg     = 11.25 pies-lbs

        A continuación se discutirá el trabajo realizado por un músculo cuya longitud promedio de su fibra muscular se conoce y su sección transversal fisiológica (STF) se ha determinado:

ECUACIÓN/FÓRMULA:

        En pulgadas-libras (pulg-lbs) es la siguiente:

T	=	90  X  STF (en pulg2) X
		Longitud de sus Fibras (en pulg)

T	=	[90  X  STF  (en pulg2) X Longitud de sus Fibras (en pulg)]
		1 pie X  -------------       12 pulg

Concepto

        Potencia representa la cantidad de trabajo realizado por una unidad de tiempo.

Ecuación/Fórmula

        Las unidades de medida de Potencia son una combinación de una unidad de trabajo con una unidad de tiempo:

        Sistema Inglés. Las unidades de medida en el sistema inglés para Potencia incluyen las siguientes:

• Pies-Libras por minuto (pies-lbs/min): Es potencia (P) producida cuando la fuerza (F) constante de una (1) libra actúa sobre un cuerpo un objeto que se mueve verticalmente a lo largo de una distancia (d) de un (1) pie en un (1) minuto (min).

• Caballo de fuerza (CF), caballo de vapor (CV) ó "horse power" (hp): Representa aquel trabajo capaz de levantar/desplazar verticalmente un peso o masa de 75 kilogramos a la altura/distancia de un (1) metrop (m) en el tiempo de un (1) segundo (seg). Es utilizado como una unidad de potencia mecánica.

• Vatio o Watt (W): Es la potencia (P) producida por el paso de un (1) amperio de corriente que circula con una fuerza o presión electromotriz de un (1) voltio. Representa el trabajo realizado durante un (1) segundo capaz de producir/emitir la energía de un (1) Julio (J). Es la medida que describe la potencia   eléctrica producida en un cicloergómetro electromecánico.

• Kilopondio-metro por minuto (kpm/min): Representa aquella fuerza (F) requerida para mover un resistencia, peso o masa de un (1) kilogramo a través de una distancia (d) de un (1) metro en un (1) minuto (min). Se utiliza para describir la cadencia de trabajo (potencia producida) en un cicloergómetro mecánico.

Energía

Concepto

        Podemos definir energía como la capacidad para hacer trabajo.

Características

        Se dice que un cuerpo posee energía cuando éste pueda efectuar trabajo. Existen diferentes formas de energía, tales como calor, sonido, luz, eléctrica, química, atómica y mecánica. Una forma de energía puede ser convertida en otra forma. Por ejemplo, cuando una bola es golpeada por un bate, parte de la energía mecánica se convierte en energía de sonido y calor, pero nunca la energía se pierde. La energía no puede ser creada ni destruída (Ley de Conservación de la Energía). Esto implica que la cantidad total de energía que posee un cuerpo o un sistema aislado permanece constante.

Clasificación

        Existen fundamentalmente dos tipos de energía, a saber, la energía potencial y la energía cinética.

        Energía potencial. Representa la capacidad que posee un cuerpo para realizar trabajo debido a su posición o configuración. Algunos ejemplos de energía potencial incluyen aquellas posiciones donde una masa o peso se encuentra levantada o en posición erecta, tal como un clavadísta de pie en la plataforma, un arco y flecha listo para soltarse y unresorte/muelle comprimido. En todos estos casos, el cuerpo u objeto posee la capacidad para realizar trabajo. Matemáticamente, la energía potencias es producto de la fuerza de un objeto posee y la distancia sobre la cual puede actuar. Su ecuación es la siguiente:

        A continuación se presenta un ejemplo para la estimación de la energía potencial:

Problema:

Dado:

Conocido:

        Energía cinética. Es aquella energía que resulta del movimiento. Esto inplica que entre más rápido se mueva un cuerpo, mayor energía cinética posee. Además, cuando un cuerpo deja de moverse, su energía cinética se pierde. Sus ecuación/fórmula matemática es la siguiente:

EC  =    x  m  x  v2

Libros

        Aguado Jódar, X. (1993). Eficacia y Técnica Deportiva: Análisis del Movimiento Humano (pp.80-97, 197-252). Barcelona, España: INDE Publicaciones. 305 pp.

        Ahonen, J., Lahtinen T., Sandström, M., Giuliano P. & Wirhed, R. (1996). Kinesiología y Anatomía Aplicada a la Actividad Física. (pp. 212-227). Barcelona, España: Editorial Paidotribo.

        Bäumler, G. & Schneider, K. (1989). Biomecánica Deportiva: Fundamentos para el Estudio y la Práctica (pp. 55-71, 99-137). España, Barcelona: Ediciones Martinez Roca, S.A..

        Brancazzio, P. (1984). Sport Science: Physical Laws and Optimum Performance (pp. 56-82, 160-179, 317-336, 347-379) New York: Simon and Schuster.

        Barham, J. N. (1978). Mechanical Kinesiology (pp. 237-249, 287-299, 300-311, 312-324, 414-421, 422-433, 434-443, 444-455, 456-465). Saint Louis: The C.V. Mosby Company.

        Bueche, F. J. & Hecht, E. (2000). Física General (9na. ed., pp.1-15, 35-56-67, 89-100, 113-127). México: McGRAW-HILL.

       Casas Reyes, J.V.,  Muñoz Quevedo, J. & Quiroga Chaparro, J. (1977). Física: Cinemática-Dinámica y Energía (pp. 129-174). México: Editorial Limusa.

        Cooper, J. M., Adrian, M., & Glassow, R. B. (1982). Kinesiology (5ta. ed., pp. 66-75, 84-86, 8-91, 324-335). St. Louis: The C. V. Mosby Company.

        Enoka, R. M. (1994). Neuromechanical Basis of Kinesiology (2nd. ed., pp.35-65, 81-87, 102-130) Champaign, IL: Human Kinetics.

        Ecker, Tom. Track and Field Dynamics (2da. ed.pp. 21-24, 26-31, 49-50, 96-102). California: Tafnews. Press, 1974.

        Gardiner, M. D. (1980). Manual de Ejercicios de Rehabilitación (Cinesiterapia)
(pp.9-10, 19-20, 22-24). España, Barcelona: Editorial JIMS.

        Gench, B. E., Hinson, M. M., & Harvey, P. T. (1995). Anatomical Kinesiology (pp.30-35, 45-49). Dubuque, Iowa: eddie bowers publishing, inc.

        Gowitzke, B. A., & Milner, M. (1988). Scientific Bases of Human Movement (3ra. ed., pp. 61-82, 93-103). Baltimore: Williams & Wilkins.

        Hall, S. J. (1999). Basic Biomechanics (3ra. ed., pp. 57-104, 165-187). Boston: The McGraw-Hill Companies, Inc.

        Hamill, J., & Knutzen, K. M. (1995). Biomechanical Basis of Human Movement (pp.
392-425). Baltimore: Williams & Wilkins.

        Hochmuth, G. (1984) Biomechanics of Athletic Movement. (pp. 26-38), 65-90, 120-153).German Democratic Republic: Sportverlag Berlin.

        Kreighbaum, E., & Barthels, K.M. (1981). Biomechanics: A Qualitative Approach for Studying Human Movement (pp.11-24, 43-49, 57-62, 69-78, 274-285, 297-319, 406-410, 414-445). Minneapolis, Minn.: Burgess Publishing Company.

        Lehmkuhl, L. D. & Smith, L. K. (1983). Brunnstrom's Clinical Kinesiology. (4ta. ed., pp. 24-33, 50-54, 61-63) . Philadelphia: F.A. Davis Company.

        Leveau, B. F. (1985). Basic biomechanics in sports and orthopaedic therapy". En: J. A. Gould III & G. J. Davies (Eds). Orthopaedic and Sports Physical Therapy (Vol II, pp.65-83). St Louis: The C.V. Mosby Company.

        Luttgens, K., & Hamilton, N. (1997). Kinesiology: Scientific Basis of Human Motion (9na. ed., pp. 340-380). Madison, WI: Brown & Benchmark Publishers.

        Norkin, C. C., & Levangie, P. (1983). Joint Structure & Function: A Comprehensive Analysis (pp. 10-36, 49-51). Philadelphia: F. A. Davis Company.
 
        Rash, P. J. & Burke, R. K. (1985). Kinesiología y Anatomía Aplicada: La Ciencia del Movimiento Humano (pp. 75-77, 79-82, 84-87, 94-98). Buenos Aires: EL ATENEO.

        Soderberg, G. L. (1986) Kinesiology: Application to Pathological Motion. (pp. 4-5, 10-12, 17-19). Baltimore: Williams & Wilkins.

        Thompson, C. W. & Floyd, R. T. (1996). Manual de Kinesiología Estructural (pp. 210-215, 218-219). Barcelona, España: Editorial Paidotribo.

        Weineck, J. (1995). La Anatomía Deportiva (pp. 70-74). Barcelona, España: Editorial Paidotribo.

        Wiktorin, C. V. Heijne & Nordin, M.(1986). Introduction to Problem Solving in Biomechanics (pp. 1-20, 25-31). Philadelphia: Lea & Febiger.

        Wirhed, R.(1997). Athletic Ability & the Anatomy of Motion (2da. ed., pp. 42-45, 102-132). St. Louis: Mosby.

Web

• The Kinematics of Sports: http://redbaron.bishops.ntc.nf.ca/rpearce/projects2000/poole/sports.html

Physics of Sports. volume 3.  Kinematics. Last updated on 21 April/98: http://www.phys.washington.edu/~young/208A/volume3.html

edgarl@asem.net elopateg@coqui.net

elopategui@hotmail.com elopateg@lycos.com

elopateg@inter.edu Rev. 27/febrero/2001