PROF. EDGAR LOPATEGUI CORSINO
M.A., Fisiología del Ejercicio
Universidad Interamericana de PR - Metro, Facultad de Educación,
Dept. de Educación Física
PO Box 191293, San Juan, PR 00919-1293
[Tel: 250-1912, X2286; Fax: 250-1197]
Definiciones/Conceptos
Movimiento
El acto o proceso de cambiar en espacio y tiempo de lugar o posición, volumen, o forma de un cuerpo o segmentos de éste u objeto (sistema) con respecto a algún marco de referencia.
Movimiento relativo
La relación del movimiento al objeto o punto específico de referencia (e.g., un pasajero se encuentra en reposo relativo al avión en que se encuentra, pero en movimiento relativo a la tierra).
Cinemática
Descripción geométrica (analítica y matemática) del movimiento de los cuerpos u objetos en el espacio, en términos de desplazamiento/distancia, velocidad y aceleración por unidad de tiempo, sin considerar las fuerzas balanceadas o desbalanceadas que causan el movimiento en un sistema, con el fin de establecer el tipo, dirección y cantidad de movimiento.
Cinemática lineal
Descripción del movimiento que se realiza en una línea récta, i.e., cinemática de la traslación o movimiento lineal.
Cinemática angular
Descripción del movimiento que se lleva a cabo alrededor de un puntofijo (el eje o centro de giro/rotación que mantiene su posición en el interior o exterior del cuerpo), i.e., cinemática de la rotación o movimiento angular.
Sistema
Un cuerpo o grupo de cuerpos u objetos bajo los cuales se examinará el movimiento (e.g., un brazo, todo el cuerpo, una bola, etc.).
Marco de referencia
Lugar específico donde se lleva a cabo el movimiento, el cual puede ser estático (e.g., un punto de referencia en el ambiente) o móvil (e.g., en un corredor puede ser un segmento adyacente al estudiado, la línea media del cuerpo, un punto en la cabeza, entre otros). Determina si un cuerpo esta en reposo o en movimiento.
Causas del movimiento
La magnitud de la fuerza relativa a la magnitud de la resistencia.
Movimiento Traslatorio o Lineal (Véase Figura 1 y 2)
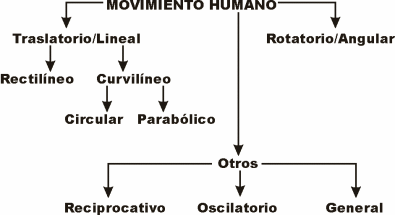
|
| Figura 2. Clasificación de los Diferentes Tipos de Movimentos. |
![]()
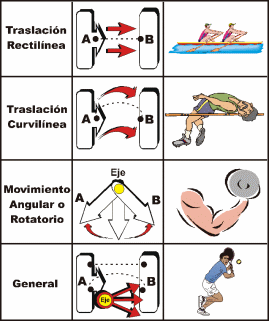
|
| Figura 2. Diferentes Tipos de Movimentos con Ejemplos. (Adaptado de: Scientific Base o Human Movemenmt (3ra. ed., p. 44), por B. A. Gowitzke & M. Milner, 1988, Baltimore, MD: Williams & Wilkins. Copyright 1988 por: Williams & Wilkins. |
Concepto.
Aquel movimiento donde el cuerpo, segmento u objeto se traslada (cambio en posición) de un lugar a otro en curvas o líneas paralelas dentro de un marco de referencia, con cada parte o puntos del cuerpo o de un objeto desplazandose en la misma dirección y por las mismas distancias.
Subclasificación.
Movimiento rectilíneo. Representa una progresión en línea recta de un cuerpo u objeto como un todo (cada punto o línea fija en el cuerpo u objeto se mantiene paralela desde su posición original/inicial hasta su posición final), de manera que todas sus partes se muevan/viajen la misma distancia, y en el mismo tiempo (velocidad uniforme). Algunos ejemplos son, a saber (véase Figura 3):

|
| Figura 3. Ejemplos de Movimentos Traslatorios Rectilíneos. |
Las unidades de medida lineales (desplazamiento lineal) se emplean para medir la distancia a través de la cual un sistema se mueve en una línea recta. Ejemplos de las unidades de medida utilizadas son pies, metros, pulgadas, centímetros, millas, kilómetros, entre otras.
Movimiento curvilíneo. Representa aquel movimiento traslatorio en el cual todas las partes del cuerpo o un objeto se mueven en curvas paralelas que transcurren en un patrón/vía irregular/variable o adopten la forma de una de las curvas definidas (e.g., parábola), de suerte que si cada curva fuese superpuesta una sobre la otra, éstas deberían coincidir exactamente (i.e., las trayectorias de las curvas paralelas son concurrentes). Sus ejemplos incluyen (véase Figura 4):

|
| Figura 4. Ejemplos de Movimentos Traslatorios Curvilíneos. |
Los movimientos curvilíneos puede seguir un patrón circular o parabólico (véase Figura 5).
|
| Figura 5. Tipos de Movimientos Curvilíneos. (Adaptado de: Mechanical Kinesiology (pp. 68-81), por J. N. Barham, 1978, Saint Louis: The C.V. Mosby Company. Copyright 1978 por: The C. V. Mosby Company. ) |
Los movimientos circulares representa aquel movimiento contínuo alrededor de la circunferencia (los límites del perímetro de un círculo) o radio (el segmento desde el centro de un círculo hasta un punto en el círculo) de un círculo. Algunos ejemplos incluyen (véase Figura 6):
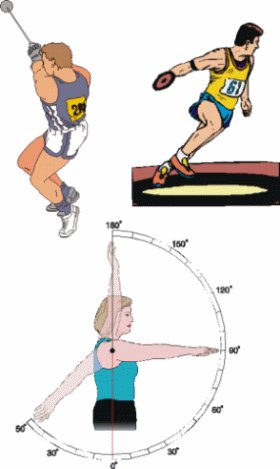
|
| Figura 6. Ejemplos de Movimientos Curvilíneos Circulares. |
El movimiento parabólico sigue una curva regular que sigue el centro de masa (o gravedad) de un cuerpo u objeto cuando es lanzado/proyectado en el aire (proyectil bajo la influencia de la fuerza de gravedad), sin ser afectado por la resistencia del aire y asu miendo que no existe ninguna otra fuerza exterior queactúe sobre el cuerpo u objeto durante su progresión. Es un movimiento que sigue un patrón de igual distancia desde un punto fijo y una línea fija. (Barham, 1978, pp. 4, 6). Sus ejemplos son:

|
| Figura 7. Ejemplos de Movimientos Curvilíneos Parabólicos. |
Movimiento Rotatorio o Angular
Concepto.
El movimiento de un objeto, cuerpo o segmentos corporales rígidos (actuando como un radio, i.e., la distancia desde el eje de rotación/giro a cualquier punto de un círculo) transcurren alrededor de un punto fijo (eje o centro de giro/rotación) y siguen la trayectoria de un círculo concéntrico, donde cada punto del sistema (objeto, cuerpo o segmento corporal) se mueve a través del mismo ángulo, al mismo tiempo, en la misma dirección y a una distancia constante/proporcional desde el eje de rotación.
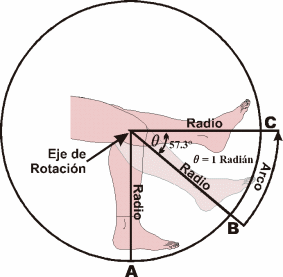
Componentes (véase Figura 10).
Eje o centro de rotación/giro. Representa la línea o punto imaginario alrededor del cual un objeto, cuerpo o segmentos de éste rotan/giran. Se encuentra en ángulo recto al plano de movimiento del cuerpo. Puede o no pasar a través del propio cuerpo. Puede hallarse dentro del cuerpo (eje interno). Por ejemplo, un bailarín girando (eje vertical que atraviesa el centro de gravedad). Además, puede encontrarse fuera del cuerpo (eje externo), tal como un gimnasta que gira alrededor de una barra horizontal (eje horizontal representado a través del centro de la barra horizontal). Las articulaciones sirven de eje de rotacion para los segmentos corporales.
Radio de rotación (de un círculo). Es la distancia lineal desde un eje de giro hasta un punto en el extremo opuesto de un objeto, cuerpo o segmento rígidos rotando. Puede ser representado por:
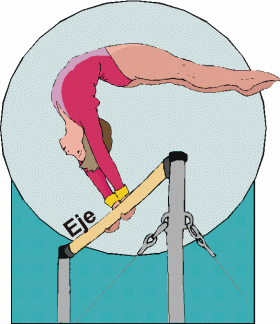
|
| Figura 8. Ejemplo de un Movimiento Angular donde Eje de Rotación se Encuentra fuera del Cuerpo. |
Ejemplos.

|
| Figura 9. Ejemplos de Movimientos Rotatorios o Angulares. |
Unidades de medida angulares (desplazamiento angular).
La función/utilidad
es medir el patrón de un cuerpo rotando. Su designación simbólica
es la letra theta (![]() ).
Algunos
ejemplos de las unidades de medida utilizadas incluyen, a saber:
).
Algunos
ejemplos de las unidades de medida utilizadas incluyen, a saber:
|
| Figura 10. Representación Esquemática de los Componentes del Movimiento de Rotación/Angular y de un Radián. El arco BC es igual en longitud al radio de la circunferencia. El radián se define como el ángulo subtendido, en un círculo, por un arco de longitud igual al radio del mismo y es equivalente a 57.3°. (Adaptado de: (Adaptado de: Joint Structure & Function: A Comprehensive Analysis (p.11), por C. C. Norkin & M. K. Levangie, 1983, Copyright 1983 por: F. A. Davis Company ) |
Otros Patrones de Movimiento
Movimiento reciprocativo.
Representa aquel patrón que denota movimientos traslatorios repetitivos. Alguno ejemplos son el movimiento rebotante de una bola y golpes repetidos de un martillo.
Movimiento oscilatorio.
Son movimientos repetidos en un arco. El péndulo, metrónomo y el diapasón son algunos ejemplos de estos tipos de movimientos.
Movimiento general.
Concepto. Los movimientos generales se caracterizan por un cuerpo u objeto que exhibe una combinación de movimientos rotatorios y traslatorios.
Ejemplos. Algunos ejemplos de movimientos generales son a saber:

|
| Figura 11. Ejemplos de Patrones de Movimiento General |
Movimiento general complejo. Son la combinación simultanea de diferentes tipos de rotaciones. Un ejemplo clásico es la acción de las piernas del ciclista. Durante este tipo de movimiento que ejecuta el ciclista existe como mínimo tres rotaciones simultaneas ejecutandose, las cuales son (Hay, 1985, p. 8):

|
| Figura 12. Ejemplo de un Movimiento General Complejo |
Existen una divesidad de factores que afectan los movimientos previeamente discutidos. Estos pueden ser de origen externo (ambiental) o interno (morfológico).
Factores Externos
Los factores externos o ambientales
que modifican el movimiento pueden ser la fricción,
reesistencia del aire y la resistencia del agua.
Factores Anatómicos (Resistencia Interna)
Bajo esta categoría se encuentra los siguientes:
En esta sección habremos de discutir varias leyes y principios de la física que atañan al movimiento de un cuerpo (o de sus segmentos) u objeto que sigue en un patrón lineal.
Desplazamiento
Concepto
El cambio en posición de un objeto o cuerpo en el espacio se conoce como desplazamiento. Se refiere a la distancia y dirección que un objeto o cuerpo se traslada desde un punto de referencia:
Cuantificación del Desplazamiento Lineal
El desplazamiento lineal comunmente se determinar mediante métodos cuantitativos. Los procedimientos cuantitativos incluyen el uso de vectores y escalas.
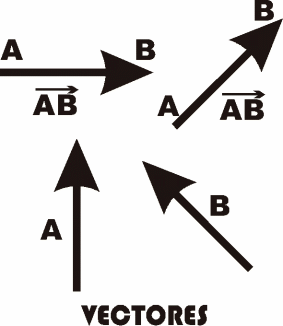
Vectores: Un vector es una medida de cantidad que posee dirección y magnitud. En términos gráficos, el vector se representa mediante un segmento rectilíneo con una flecha en el extremo de éste. Los componentes del vector pueden ser descritos como sigue:
|
La composición (combinación) de vectores representa un método para determinar una resultante vectorial. Un vector resultante es aquel nuevo vector (resultante) que se halla al combinar dos o más vectores. Por ejemplo, en la suma de dos vectores (A + B), el vector resultante (R) se consigue al unir el extremo final (flecha) de un vector (A) con el origen del otro vector (B):
![]()
|
|
Cantidad escalar. Representa aquellas cantidades que expresan únicamente un valor o magnitud (e.g., longitud o distancia).
Las unidades de medida empleadas durante las estimacionee del desplazamiento lineal son básicamente aquellas de longitud o distancia. Estas son, a saber: pies, metros, millas, kilómetros, entre otras.
Cálculo del Desplazamiento Lineal
Forma general. Midiendo la longitud de una línea recta, uniendo sus porciones iniciales y finales y notando la dirección que dicha línea toma.
Con referente a algún eje x arbitrario. El desplazamiento es la diferencia entre las coordenadas terminal e inicial del objeto o cuerpo sobre la escala:
| d = xt - xi |
| Donde:
d = desplazamiento lineal
|
Ejemplo (véase figura 3)
Situación:
| Una persona que camina hacia el norte recorriendo 3 kilómetros hasta un punto B y luego hacia el este a través de 4 kilómetros hasta un punto C. Este individuo ha caminado una distancia de 7 kilómetros (3 km + 4 km = 7 km). |
Dado:
| AB (Opuesto) = 3 km
BC (Adyacente) = 4 km |
Conocido:
Desplazamiento lineal:
| d = xt - xi |
Teorema de Pitágoras:
| En todo triángulo rectángulo el cuadrado de la longitud
de la hipotenusa es igual a la suma de los cuadrados de las longitudes
de los catetos (opuesto y adyacente):
AB2 (Hipotenusa) = AB2 + BC2 |
Problema: ¿Cuanto es el desplazamiento con respecto al punto inicial (en kilómetros)?:
Empleando la fórmula para el Teorema de Pitágoras:
| AB2 = AB2 + BC2
AB2 = 32 + 42 AB2 = 9 + 16 AB2 = 25 AB = AB = 5 km |
Rapidez
Concepto
La rapidez representa una cantidad escalar (posee solo magnitud) que indica la distancia que un objeto o cuerpo recorre/viaja en un tiempo dado. Da a conocer solamente cuan rápido un objeto o cuerpo se mueve. Es la magnitud de la velocidad.
Cálculo de la la Rapidez
La rapidez se puede estimar al determinar la distancia total recorrida por el objeto o cuerpo y dividiéndola entre el tiempo que toma cubrir dicha distancia. Su ecuación puede ser expresada como sigue:
| d
--- t |
| donde:
|
Ejemplos
A continuación varias formas de espresar la rapide:
Concepto
La velocidad reprsenta la proporción en el cambio de la posición del objeto o cuerpo (desplazamiento) con respecto al tiempo empleado. Es la rapidez y dirección de un cuerpo.
Características
La velocidad es una cantidad vectorial. Involucra dirección así como rapidez. Es rapidez en una dirección dada. La dirección de la velocidad es la misma que la del vector desplazamiento.
Unidades de Velocidad
Se emplean unidades de longitud sobre unidad de tiempo. En estudios humanos, se utilizan las siguiente unidades de medida:
| Centímetros
------------- = Segundo |
cm
----- seg |
; | Pulgadss
---------- = Segundo |
pulg
----- seg |
| Metros
------------- = Segundo |
m
----- seg |
; | Pies
---------- = Segundo |
pie
----- seg |
Al describir velocidadea a través de largas distancias, entonces comunmente se utilizzan las siguientes unidades de medida:
| Kilómetros
------------- = Hora |
km
----- hr |
; | Millas
---------- = Hora |
mi
----- hr |
Cálculo de la Velocidad
La velocidad se puede estimar dividiendo el desplazamiento de un objeto o cuerpo entre la cantidad de tiempo transcurrido durante dicho desplazamiento. Su ecuación es la siguiente:
| d
--- t |
| donde:
|
Ejemplo
Problema:
| Determinar la velocidad promedio de una bola de tenis en el servicio. |
Dado:
| Desplazamiento de la Bola (d) = 58 pies
Tiempo Transcurrido (t) = 0.35 segundos |
Conocido:
Velocidad Promedio:
| d
t |
Solución:
| d
t 58 pies
|
Aceleracion
Concepto
La aceleración reprsenta el cambio proporcional en velocidad con respecto al tiempo transcurrido. La aceleracion media/promedio es la razón entre el cambio de velocidad y el intervalo de tiempo.
Características
Las unidades de aceleración seran aquellas de velocidad/tiempo o rapidez/tiempo más una direccion. A continuación algunos ejemplo:
La aceleración lineal promedio se expresa matemáticamente mediante la siguiente ecuación:
| vf - vi
----------- t |
| donde:
|
Ejemplo
Problema:
| Calcular la aceleración lineal promedio de un nadador. |
Dado:
| Velocidad inicial (vi) = 0 m.seg (en el momento
del disparo Velocidad final (vf) = 1.8 m.seg (dos segundos luego de haber comenzado la carrera) |
Conocido:
Aceleración Promedio:
| vf
- vi
t |
Solución:
| vf
- vi
t 0 m/seg
- 1.8 m/seg
1.8 m/seg
|
Desplazamiento Angular
Concepto
El desplazamientio angular
de sefine como cualquier objeto o cuerpo, que actuando como una barra/segmento
rígido, se mueve en un arco alrededor de un eje. También
se conoce como el recorrido/movimiento rotatorio de un objeto o cuerpo
de una posición a otra. Equivale a la magnitud de los dos ángulos
mas pequenos entre las posiciones inicial y final de un objeto o cuerpo.
La letra Griega theta (![]() )
es el símbolo empleado para representar el desplazamiento angular.
)
es el símbolo empleado para representar el desplazamiento angular.
Distancia Angular
Cuando un objeto o cuerpo rotando se mueve de una posición a otra. la distancia angular equivale al ángulo entre sus posiciones inicial y final. Es una cantidad escalar, puesto que solo posee solamente magnitud.
Dirección del Desplazamiento Angular (véase Figura 21)
El desplazamiento angular puede estar orientado a favor de las manecillas/agujas del reloj (negativo) o en contra de las manecillas/agujas del reloj (positivo).
Unidades de Medida
Unidades rotatorias o angulares de desplazamiento. Esta son las siguientes:
| C = 2 |
| Donde:
C = longitud de la circunferencia del círculo
|
Relaciones entre grados, radianes y revoluciones (factores de conversión angulares): A continuación las equivalencias de las variables que posee un círculo:
| 360 grados = 2 180 grados = 1 90 grados = 1 grado = 1 radián = 57.30 grados = 0.16 revolución 1 revolución = 360 grados = 2 |
Conversión de un desplazamiento angular a un desplazamiento lineal: Para éesto propósitos se emplea la siguiente fórmula:
| d = r |
| Donde:
d = desplazamiento lineal (distancia lineal
de un punto sobre un segmento rotando
|
Desplazamiento Angular en un Tiempo Dado
Corresponde a una distancia lineal. Se expresa como sigue:
| Donde:
|
Rapidez Angular
Concepto
La rapidez angular representa la proporción en el cambio de posición (distancia cubierta) de un objeto, cuerpo o segmento rígido (actuando como un radio) que gira/ rota alrededor de un ángulo (i.e., el radio barre/recorre el ángulo) en una unidad de tiempo. Indica cuan rápido un objeto, cuerpo o segmento rígido (actuando como un radio) se desplaza a través de un ángulo, en rotaciones. Puede también definirse como la magnitud de la velocidad angular.
Características
La rapidez angular posee las siguientes propiedades:
Es una cantidad escalar: Similar a la rapidez lineal, la rapidez angular representa una cantidad escalar puesto que posee únicamente magnitud.
Arco recorrido por cada punto del radio (movimiento de cada parte o punto a lo largo del objeto, cuerpo o segmento rígido desde el eje o centro de rotación). Cada punto a lo largo del objeto, cuerpo o segmento rígido (radio) viajan a través de diferentes distancias lineales, de manera que cada punto también poseen distintos niveles de rapidez lineal. Esto implica que los puntos que se mueven con mayor rapidez lineal son los situados a mayor distancia del eje de giro, por tener que recorrer una distancia mayor en igual intervalo de tiempo. Por lo tanto, un punto en el extremo del objeto, cuerpo o segmento (donde se encuentra la circunferencia del círculo) posee mayor rapidez lineal que un punto más cerca del centro de rotación. En otras palabras, en un objeto, cuerpo o segmento rígido (radio) rotando, entre más lejos un punto de dicho radio se encuentre del centro de rotación (o eje de giro), más rápido linealmente se moverá, ya que recorre una mayor distancia en el mismo intervalo de tiempo, en comparación con los otros puntos del radio que se hallan más cerca del centro de giro. Por consiguiente, de deriva el siguiente principio: la rapidez lineal de cualquier punto en un objeto, cuerpo o segmento rotando se encuentra en proporción directa (directamente relacionado) a su distancia de rotación.
Angulo barrido por
el radio (ángulo que recorren cada punto del objeto, cuerpo o segmento
rígido). Todas las partes o puntos a lo largo de un objeto,
cuerpo o segmento rígido (actuando como un radio) rotando, poseen
la misma rapidez angular (i.e., todos los puntos del radio se mueven con
igual desplazamiento/distancia angular o rapidez angular), ya que el arco
recorrido por todos los puntos del radio barren el mismo ángulo
(véase figura 19 y 20). Esto qiere decir que cada punto del objeto,
cuerpo o segmento rígido (radio) se mueve a través del mismo
ángulo (un mismo ángulo barrido simultáneamente por
la recta o radio que contiene los diversos puntos) y realiza el mismo número
de revoluciones.
Unidades de Medida
Unidades de ángulo dividido por tiempo. Alguno ejemplo incluyen las siguientes unidades más comunes:
| grados/hr | grados |
| radianes/hr | radianes/seg |
Frecuencia angular o rotatoria. Es una medida de la proporcion rotatoria, i.e., el número de revoluciones completas (veces en que se recorre o se le da vuelta a 360 grados) calculadas alrededor de un patrón circular durante un intervalo de tiempo dado a una rapidez periférica (angular) constante. La frecuencia rotatoria es útil cuando en movimientos rotatorios la rapidez periférica (angular) es constante. sus unidades son:
| 1 Hz = | 1 rev
----------- seg |
| f = | # rev
----------- t |
| donde:
f = frecuencia angular
|
Ecuación/Fórmula para la Rapidez Angular
La ecuación para rapidez angular es la siguiente:
| Donde:
|
Ejemplo
Problema:
| Determinar la rapidez angular del planeta tierra |
Dado:
| Desplazamiento Angular de la Tierra ( Tiempo Transcurrido ( |
Conocido:
Aceleración Promedio:
Solución:
360°
|
Velocidad Angular
Concepto
La velocidad angular se puede definir como la proporción del desplazamiento angular/rotatorio por el radio, en una dirección específica, durante un tiempo dado. Tambiés puede describirse como la variación del ángulo sobrepasado/recorrido por el objeto, cuerpo o segmento actuando como una barra rígida (radio), el cual se mueve alrededor de un eje/centro giratorio/rotatorio, en una dirección específica y durante un periodo de tiempo particular. La rapidez angular en una dirección dada también define en forma sencilla el término de velocidad angular.
Características
Es una cantidad vectorial que especifíca. La velocidad angular representa una cantidad vectorial puesto que posee las siguientes propiedades: (1) rapidez (magnitud) de la rotación alrededor de su eje y (2) dirección espacial (a favor o en contra de las agujas del reloj) de su eje de rotación.
Factor de dirección en la velocidad angular (véase figura 21). El componente de dirección espacial en la velocidad angular se caracteriza por ser encontra (positivo) o a favor (negativo) de las manecillas del reloj:
| v = r |
| Donde:
v = velocidad lineal (de un punto sobre un segmento/palanca
rotando).
|
Esto implica (véase figura 18, 19 y 20) que entre más grande sea la velocidad angular y mayor sea la longitud de la palanca (radio), mayor será la velocidad lineal en el extremo de la palanca (radio).
Todos los puntos del radio recorren la misma distancia. La distancia angular recorrida por cada punto puntos en el radio del círculo, sin importar donde se localizan en relación al eje, es la misma (véase figura 18, 19 y 20).
Efectos de Variar la Longitud del Radio de Rotación sobre la Velocidad Angular
- Bajo esta propiedad que posee la velocidad angular, se rigen los siguientes principios:
| v = r |
| v
--- r |
- A
continuación se describen aquellas situaciones en las cuales el
alargamiento del
radio es deseado:
La velocidad angular se expresa en forma matemática mediante la siguiente ecuación:
![]()
--- t |
| donde:
t = tiempo que toma para el desplazamiento
|
Ejemplo
Problema:
| Determinar la velocidad angular de un palo de "golf" durante la oscilación de éste para golpear la bola. |
Dado:
| Desplazamiento Angular del Palo de "Golf" ( Tiempo que Tomó el Desplazamiento Angular (t) = 0.09 segundos |
Conocido:
Velocidad angular:
t |
Solución:
t 2.8 radianes
|
Aceleración Angular
Concepto
Podemos definir aceleración angular como la proporción en tiempo del cambio en la velocidad angular de un sistema.
Característica
La magnitud de la aceleración o desaceleración de un segmento o implemento (e.g., bate, raqueta, entre otros) rotando determina cuan rápido dicha velocidad se alcanza.
Ejemplo
Movimientos segmentales del cuerpo humano. Cada vez que un movimiento segmental del cuerpo se inicia, ha sido acelerado o desacelerado angularmente. Los determinantes para la magnitud de la aceleración de un segmento corporal son, a saber:
La aceleración angular promedio se define mediante la siguiente relación matemática:
----------- t |
| donde:
|
Relación entre el Movimiento Lineal y el Movimiento Angular
Principios
Para cualquier velocidad
angular dada, la velocidad lineal es directamente proporcional al radio
(véase figura 25, 26 y 27). Dicho en otra forma, la velocidad lineal,
del movimiento circular/rotatorio, en el extremo de la palanca (o radio)
es directamente proporcional a la longitud de dicha palanca/radio (que
puede ser un objeto, cuerpo o segmento actuando como una barra fija), siempre
y cuando la velocidad angular se mantenga constante. Esto significa que
entre más largo sea la palanca o radio (distancia entre el eje/centro
de giro y el punto de contacto o extremo de la circunferencia del círculo)
de un implemento deportivo (e.g., bate, raqueta, palo de "golf") y/o segmento/extremidad
del cuerpo, mayor velocidad lineal es generada en su extremo, en igualdad
de condiciones. Alguno ejemplos de etos principios de ilustran en las figuras
25, 26 y 27.
En conclusión, Para poder alcanzar mayores velocidades lineales
en el extremo de las palancas (radios), los movimientos deben de realizarse
con palancas (radios) más largas o mayores velocidades angulares
(véase ejemplo ilustrado en la figura 28). El determinante para
escoger un implemento deportivo con la longitud óptima es la habilidad
individual para mantener la velocidad angular (véase ejemplo en
la Figura 29).
| Aumento Doble del Radio
Aumento Doble de la Velocidad Lineal |
(Si la Velocidad Angular Se Mantiene Constante)
|
| Figura 25 |
![]()
(En Igualdad de Condiciones)
|
| Figura 26 |
![]()
|
![]()
Velocidad Lineal se Mantiene Constante
|
Una vez el objeto (palanca) se haya encaminado en el movimiento circular/rotatorio (angular), la velocidad lineal en el extremo del radio (o palanca) se mantiene igual debido a la conservación del momentum.
Para cualquier velocidad lineal dada, la velocidad angular es inversamente proporcional al radio (véase Figura 30). Dicho en otra forma, cuando la velocidad lineal se mantiene constante, aumentando el largo del radio reduce la velocidad angular y acortando el largo del radio aumenta la velocidad angular (véase figura 31). Algunos ejemplos se ilustran en las Figuras 32 y 33.
Para poder alcanzar velocidades lineales altas en los extremos de las palancas (radios), el movimiento debe ejecutarse con palancas (radios) más largos y/o a mayores velocidades angulares (véase Figuras 28 y 34).
![]()
| Aumento Doble del Radio
Reducción a la Mitad de la Velocidad Angular |
| Figura 30 |
![]()
| Velocidad Lineal se Mantiene Constante
|
![]()
|
| Figura 32.Un Ejemplo de Como La Longitud del Radio de Rotación Afecta la Velocidad Angular |
![]()
|
![]()
|
| Figura 34. |
Proyecciones Verticales
Factores que Gobiernan el Vuelo de un Objeto Lanzado hacia Arriba
La fuerza o velocidad del lanzamiento hacia arriba. El objeto bajando es acelerado a la misma proporción que cuando fue lanzado hacia arriba. Entre mayoy sea la velocidad inicial de la proyección hacia arriba, mayor será la altura máxima (Cumbre) alcanzada por el objeto. Por ejemplo:
| Velocidad Inicial de
un Objeto Lanzado Hacia Arriba |
Altura Máxima Alcanzada
(Velocidad Cero) |
Tiempo Tomado para
la Altura Máxima |
| 32 pies/seg | 16 pies | 1 segundo |
| 64 pies/seg | 64 pies | 2 segundos |
| 96 pies/seg | 144 pies | 3 segundos |
La fuerza de gravedad hacia abajo. Objetos proyectados hacia arriba son desacelerados por la fuerza de gravedad hacia abajo.
| Objeto Lanzado Hacia Arriba
El Objeto va Desacelerando debido a la Fuerza de Gravedad Punto donde la Fuerza de Gravedad hacia Arriba es Neutralizada por la Fuerza de Gravedad hacia Abajo El Objeto Alcanza una Altura Máxima (Cumbre o Pico) (Velocidad Resultante = 0) El Objeto Cae a un Velocidad de 32 pies/seg cada Segundo que esta en el Aire |
| Figura 35. Factores que Gobiernan el Vuelo de un Objeto Lanzado Hacia Arriba |
![]()
Fuerza de Proyección hacia Arriba (Velocidad Inicial hacia Arriba)
|
![]()
| Objeto Lanzado Horizontalmente
Comienza Horizontalmente Fuerza de Gravedad Ejerce Efecto Adicional sobre el Objeto Inmediátamente Después sigue un Patrón de Curva hacia abajo |
| Figura 37. Factores que Gobiernan el Vuelo de un Objeto Lanzado Hacia Arriba - Influencia de la Fuerza e Gravedad |
Proyecciones Horizontales
Factores que Gobiernan el Patrón de Vuelo de Objetos Lanzados hacia Horizontalmente
La fuerza del lanzamiento. La fuerza o velocidad horizontal sobre un objeto proyectado horizontalmente es independiente de la fuerza de la velocidad vertical del objeto. Afecta solo la distancia horizontal que un objeto puede recorrer mientras se mantiene en el aire antes de golpear el suelo. La distancia vertical hacia abajo será igual siempre, puesto que la caída depende enteramente del tiempo que la gravedad tiene para actuar sobre el objeto y la aceleración debido a que la gravedad cambia.
La fuerza de gravedad hacia abajo.
Proyecciones Diagonales
Factores que Determinan el Vuelo de un Objeto Proyectado Diagonalmente
La velocidad horizontal. La velocidad horizontal resultante del vuelo de un objeto proyectado diagonalmente se mantiene constante debido a que no existe ninguna otra fuerza horizontal introducida que pueda alterar dicha velocidad horizontal resultante (excluyendo la resistencia del aire).
La velocidad vertical. Los factores que determinan la velocidad vertical resultante del vuelo de un objeto proyectado diagonalmente son:
Factores que Determinan ls Magnitud del Componente Horizontal y el Componente Vertical
La velocidad de la proyección.
El ángulo de la proyección. Conforme se reduce el ángulo, el componente horizontal aumenta y el componente vertical se reduce, y viceversa (véase Figura 38).
|
|
| Figura 38. Relación entre el Ángulo de Proyección y los Componentes Horizontales y Verticales |
Ángulo Ópimo para la Proyección de un Misil
Se ha encontrado que es 45 grados. El punto de aterrizaje se encuentra al mismo nivel de altura donde se liberó el misil.
Ángulo Ópimo para la Implementos Lanzados
Bajo estas circuntancias, el ángulo óptimo debe ser menor de 45 grados. Esto se debe a que todos los implementos lanzados son liberados sobre el nivel de la tierra.
Factores que Determinan el Ángulo Ópimo de Vuelo
Esto dependerá del propósito de la trayectoria. Si el tiempo en que el objeto se mantendrá en el aire es importante, entonces el ángulo óptimo se hallará enter 70° y 60°. Es detrimenmtal, cuando el aire y la resistencia del viento alteran el vuelo del objeto. En este caso, el ángulo óptimo sería de 20° a 30°. Por el otro lado, si la velocidad en que el objeto debe llegar a su destino es lo más importante para el atleta, entonces entre más agudo el ángulo de proyección mejor será (trayectoria plana del objeto).
Factores que Determinan la Distancia Recorrida de un Objeto Lanzado
El ángulo de liberación. 45° es el ángulo óptimo a través del cual el objeto podrá recorrer la mayor distancia horizontal (asumiendo que el nivel de liberación es el mismo que el de aterrizaje y excluyendo la resistencia del aire).
La altura de la liberación. Entre mayor sea la altura de la liberación, mayor deberá ser la reducción del ángulo óptimo de 45° con el fin de poder recorrer una mayor distancia.
La velocidad de la liberación. En igualdad de condiciones, entre mayor sea la velocidad inicial, menor será la necesidad de reducir el ángulo óptimo de 45° y mayor distancia podrá recorrer el objeto.
Fuerzas aerodinámicas.
Para poder recorrer una mayor distancia, los ángulos de liberación
en el disco y jabalina (los cuales no siguen una parábola perfecta)
deben ser menores (30° a 40°) que el martillo y la bala (40°
a 44°), los cules siguen una parábola perfecta.
Libros
Aguado Jódar, X. (1993). Eficacia y Técnica Deportiva: Análisis del Movimiento Humano (pp. 130-165). Barcelona, España: INDE Publicaciones. 305 pp.
Ahonen, J., Lahtinen T., Sandström, M., Giuliano P. & Wirhed, R. (1996). Kinesiología y Anatomía Aplicada a la Actividad Física. (pp. 227-229). Barcelona, España: Editorial Paidotribo.
Bäumler, G. & Schneider, K. (1989). Biomecánica Deportiva: Fundamentos parael Estudio y la Práctica (pp. 15, 25-53). España, Barcelona: Ediciones Martinez Roca, S.A..
Brancazzio, P. (1984). Sport Science: Physical Laws and Optimum Performance (pp. 25-55, 281-317, 337-346). New York: Simon and Schuster.
Barham, J. N. (1978). Mechanical Kinesiology (pp. 189-204). Saint Louis: The C.V. Mosby Company.
Bueche, F. J. & Hecht, E. (2000). Física General (9na. ed., pp. 16-31, 130-131). México: McGRAW-HILL.
Casas Reyes, J.V., Muñoz Quevedo, J. & Quiroga Chaparro, J. (1977). Física: Cinemática-Dinámica y Energía (pp. 73-128). México: Editorial Limusa.
Cooper, J. M., Adrian, M., & Glassow, R. B. (1982). Kinesiology (5ta. ed., pp. 75-83, 176-177). St. Louis: The C. V. Mosby Company.
Enoka, R. M. (1994). Neuromechanical Basis of Kinesiology (2nd. ed., pp. 3-33 ) Champaign, IL: Human Kinetics.
Ecker, Tom. Track and Field Dynamics (2da. ed. pp. 18-21, 24,32-48, 61-79, 90-95). California: Tafnews. Press, 1974.
Gardiner, M. D. (1980). Manual
de Ejercicios de Rehabilitación (Cinesiterapia)
(pp.2-6, 10-12). España, Barcelona: Editorial JIMS.
Gench, B. E., Hinson, M. M., & Harvey, P. T. (1995). Anatomical Kinesiology (p.8). Dubuque, Iowa: eddie bowers publishing, inc.
Gowitzke, B. A., & Milner, M. (1988). Scientific Bases of Human Movement (3ra. ed., pp. 43-60). Baltimore: Williams & Wilkins.
Hall, S. J. (1999). Basic Biomechanics (3ra. ed., pp. 13-56). Boston: The McGraw-Hill Companies, Inc.
Hamill,
J., & Knutzen, K. M. (1995). Biomechanical Basis of Human Movement
(pp.
326-391). Baltimore: Williams & Wilkins.
Hochmuth, G. (1984) Biomechanics of Athletic Movement. (pp. 12-26). German Democratic Republic: Sportverlag Berlin.
Kreighbaum, E., & Barthels, K.M. (1981). Biomechanics: A Qualitative Approach for Studying Human Movement (pp.24-25, 50-57, 285-297, 336-342, 379-406). Minneapolis, Minn.: Burgess Publishing Company.
Lehmkuhl, L. D. & Smith, L. K. (1983). Brunnstrom's Clinical Kinesiology. (4ta. ed., pp.1-2, 5-6) . Philadelphia: F.A. Davis Company.
Leveau, B. F. (1985). Basic biomechanics in sports and orthopaedic therapy". En: J. A. Gould III & G. J. Davies (Eds). Orthopaedic and Sports Physical Therapy (Vol II, pp.65-83). St Louis: The C.V. Mosby Company.
Luttgens, K., & Hamilton, N. (1997). Kinesiology: Scientific Basis of Human Motion (9na. ed., pp. 314-339). Madison, WI: Brown & Benchmark Publishers.
Norkin, C. C., & Levangie, P. (1983). Joint Structure & Function: A Comprehensive Analysis (pp. 4-7). Philadelphia: F. A. Davis Company.
Rash, P. J. & Burke, R. K. (1985). Kinesiología y Anatomía Aplicada: La Ciencia del Movimiento Humano (pp. 73-75, 77-79). Buenos Aires: EL ATENEO.
Soderberg, G. L. (1986) Kinesiology: Application to Pathological Motion. (pp. 3-5, 14-17). Baltimore: Williams & Wilkins.
Thompson, C. W. & Floyd, R. T. (1996). Manual de Kinesiología Estructural (pp. 210, 219). Barcelona, España: Editorial Paidotribo.
Wiktorin, C. V. Heijne & Nordin, M.(1986). Introduction to Problem Solving in Biomechanics (pp.xix-xx). Philadelphia: Lea & Febiger.
Wirhed, R.(1997). Athletic Ability & the Anatomy of Motion (2da. ed.,pp. 132-133). St. Louis: Mosby.
Web
|
|
edgarl@asem.net
elopateg@coqui.net |
elopategui@hotmail.com
elopateg@lycos.com |
|
| Copyright © 2001 Edgar Lopategui Corsino |